Estructuras de Datos y Algoritmos II



Clase 2



versión imprimible o pfd

Estructuras de Datos y Algoritmos II


Árboles

Repaso

¿Qué es una estructura de datos?

“ Una estructura de datos es una forma particular de organizar la información en una computadora de manera tal que pueda se usada eficientemente. ” Paul E. Black - "Dictionary of Algorithms and Data Structures"

¿Qué es un algoritmo?

“ un algoritmo es un procedimiento computacional bien definido que toma un valor/es como entrada y produce un valor/es como salida. Es por lo tanto una secuencia de pasos que transforman una entrada en una salida. ”

Inter-dependencia entre

propiedades/reglas de la estructura de datos

y los algoritmos que permite

ventajas y desventajas

Árboles

El jardin de los senderos que se bifurcan

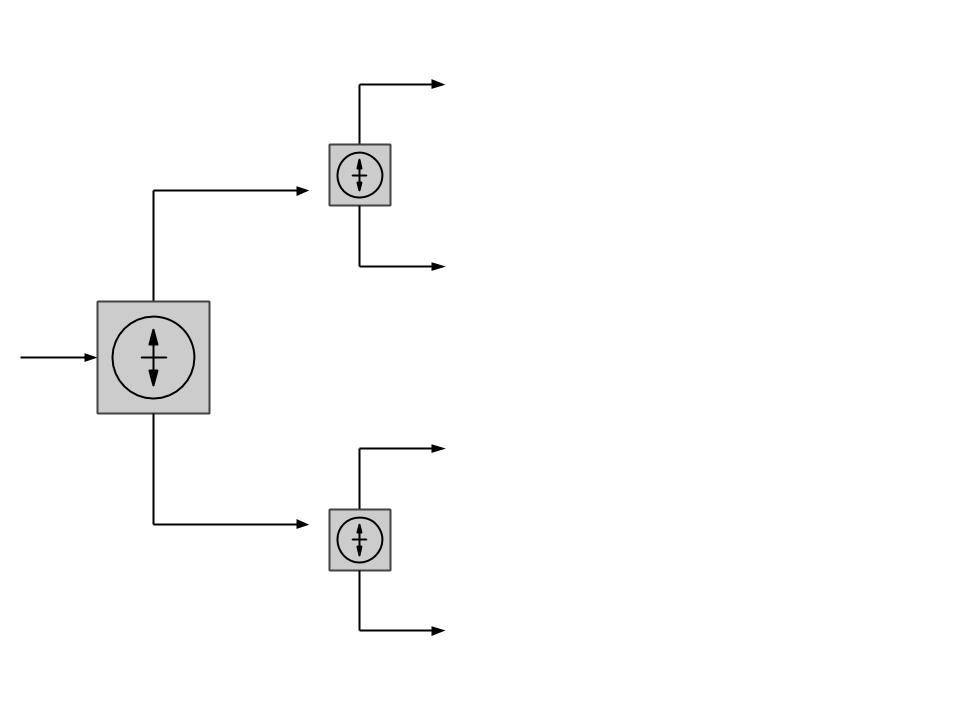
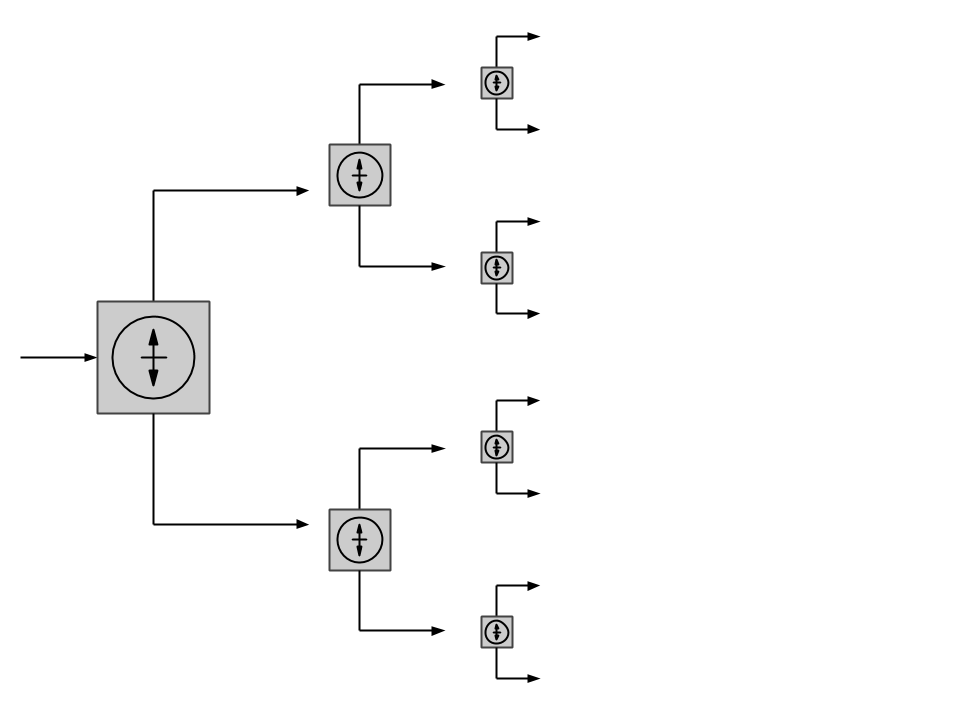
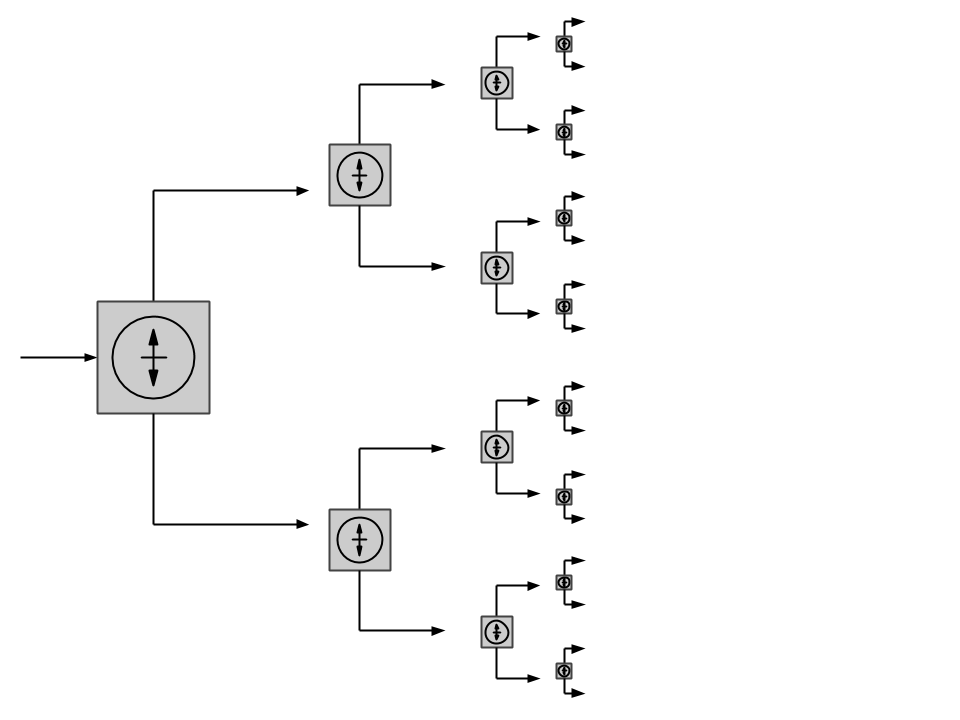
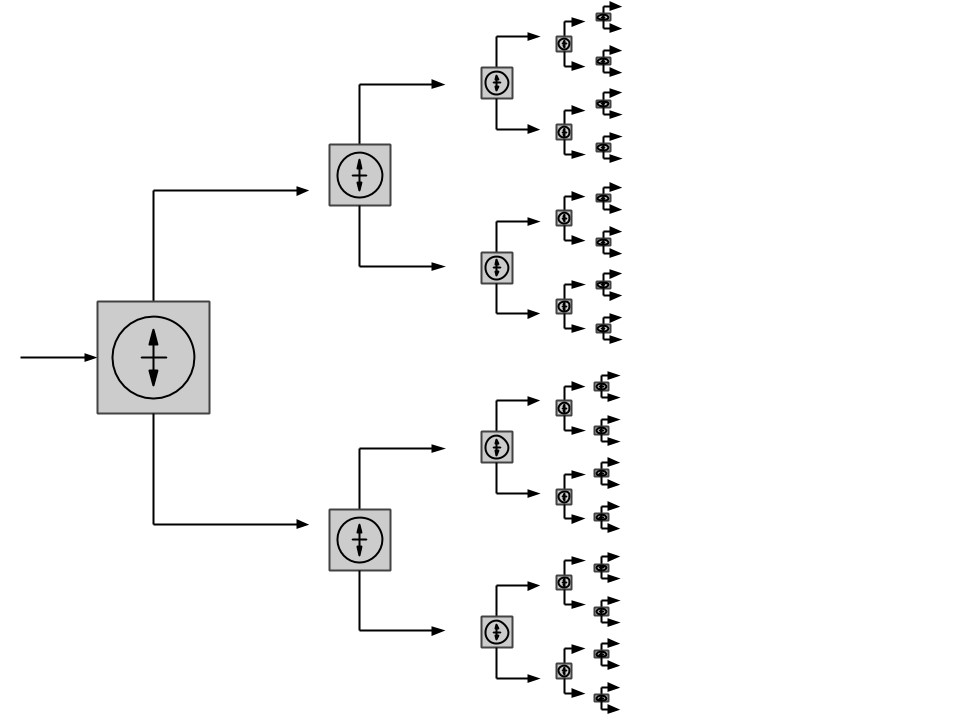
Recurrencia, recursión o recursividad es la forma en la cual se especifica un proceso basado en su propia definición.








    Recursión

Definición

Es una colección de nodos, tal que:

  • puede estar vacía
  • o puede estar formada por un nodo (raíz) y otros dos árboles T1 y T2, dónde la raíz de cada árbol Ti está conectado a R por medio de una arista.



https://en.wikipedia.org/wiki/List_of_data_structures#Trees

Términos

nodo, arista, raíz, hoja, subárbol

padre, hijos, hermanos

camino

desde n1 hasta n k , es una secuencia de nodos n 1 , n 2 , ....,n k tal que n i es el padre de n i+1 , para 1 ≤ i < k.

La longitud del camino es el número de aristas, es decir k-1. Existe un camino de longitud cero desde cada nodo a sí mismo. Existe un único camino desde la raíz a cada nodo

profundidad de un nodo

Es la longitud del único camino desde la raíz hasta el nodo.

La raíz tiene profundidad cero.

altura de un nodo

longitud del camino más largo desde el nodo hasta una hoja.

Las hojas tienen altura cero.

La altura de un árbol es la altura del nodo raíz.

Grado de un nodo:

es el número de hijos del nodo

Ancestros y Descendientes

N1 es ancestro de N2 y N2 es descendiente de N1, si existe un camino desde N1 a N2

Aplicaciones

Árboles binarios de búsqueda

Árboles de expresión

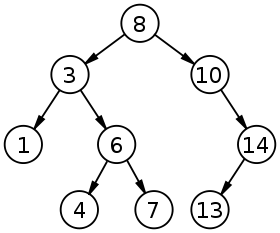
Árboles binarios de búsqueda

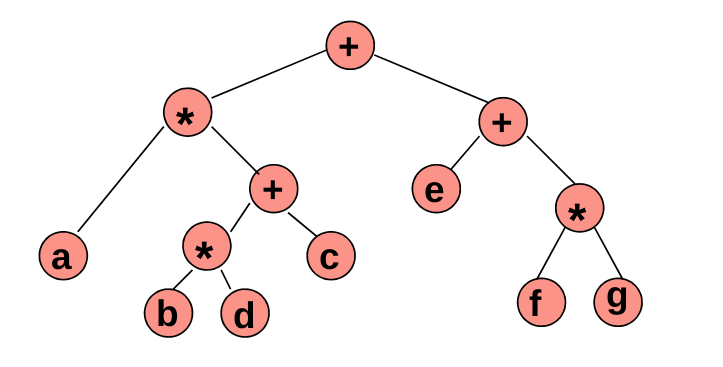
Árboles de expresión 


                          a * b + c
    
    
                          a * ( b + c )

a * ( ( b * d ) + c ) ) + ( e + ( f * g ) )

Recorridos

En profundidad (DFS): inorden, preorden, postorden

por niveles (BFS)

preorden


            1. proceso la raiz
            2. Si tengo hijo izquierdo, recorro el subarbol izquierdo
            3. Si tengo hijo derecho, recorro el subarbol derecho

inorden


            1. Si tengo subarbol izquierdo, recorro el subarbol izquierdo
            2. proceso la raíz
            3. Si tengo subarbol derecho, recorro el subarbol derecho

postorden


            1. Si tengo subarbol izquierdo, recorro el subarbol izquierdo
            2. Si tengo subarbol derecho, recorro el subarbol derecho
            3. proceso la raíz

Por niveles (BFS)

utilizamos estructura auxiliar... 

            
              encolar raíz
              mientras haya nodos en la cola:
              desencolo un nodo
              proceso el nodo
              si tiene hijo izquierdo, encolo hijo izquierdo
              si tiene hijo derecho, encolo hijo derecho

Por niveles (con marca de fin de nivel)

utilizamos estructura auxiliar... 

            
              1. encolar raíz
              2. encolar marca de fin de nivel
              3. mientras la cola no sea vacía:
              3.1 desencolo un elemento
              3.2 mientras elemento no sea fin de nivel
              3.2.1 proceso el nodo
              3.2.2 si tiene hijo izquierdo, encolo hijo izquierdo
              3.2.3 si tiene hijo derecho, encolo hijo derecho
              3.2.4 desencolo un elemento
              3.3 si la cola no es vacía, encolo marca de fin de nivel

Implementación

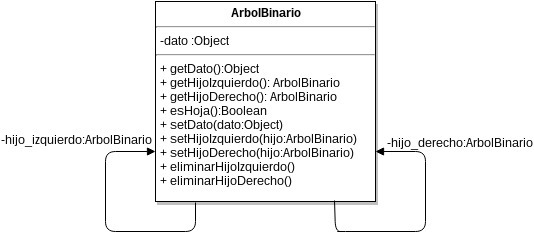
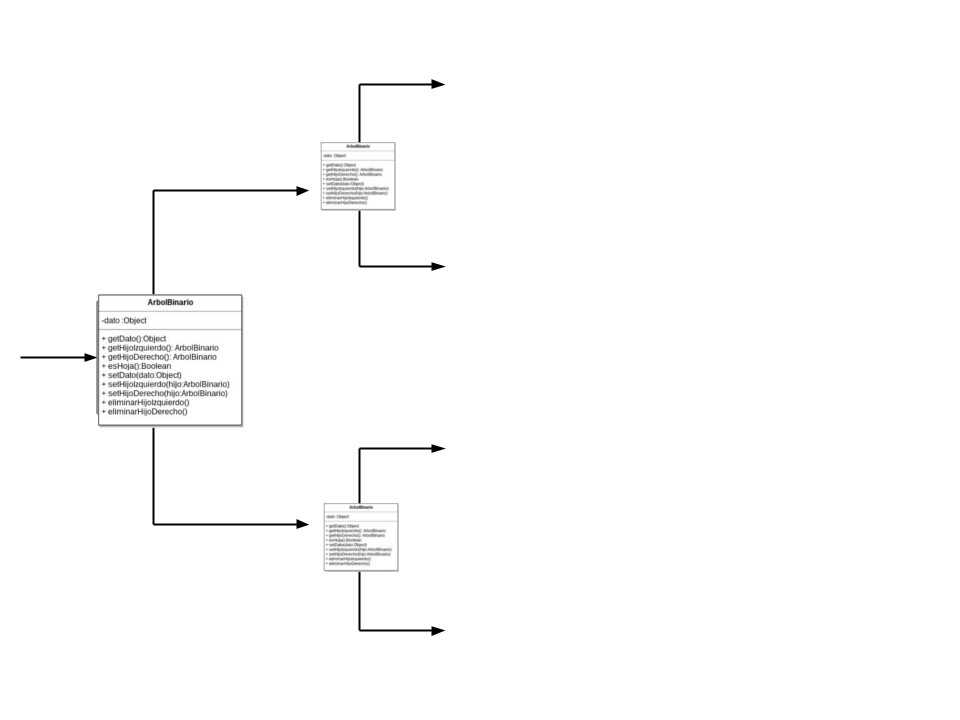
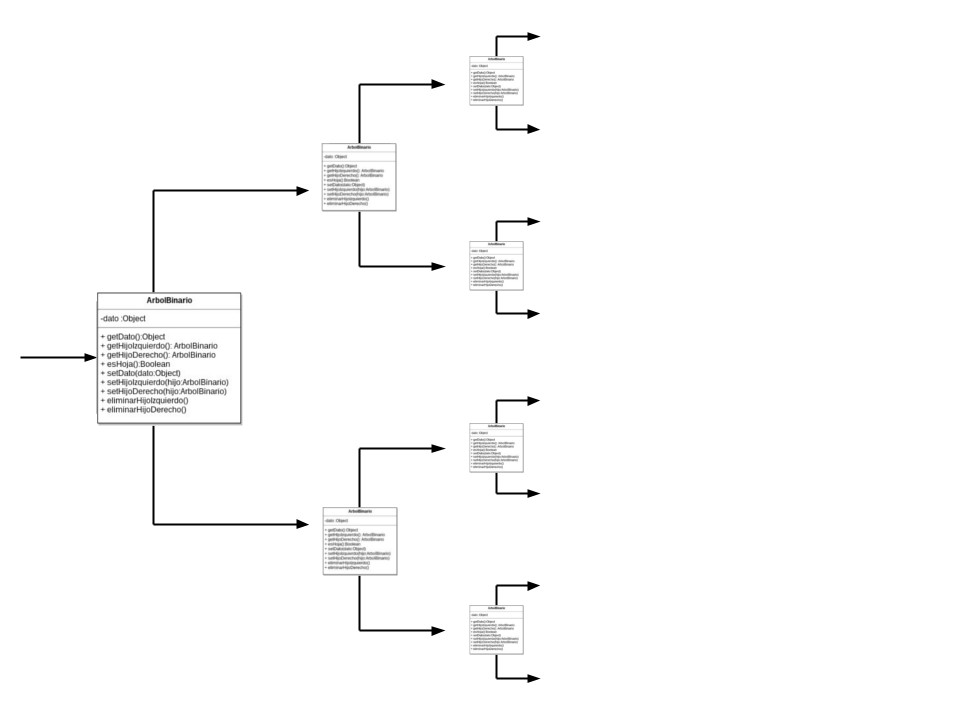
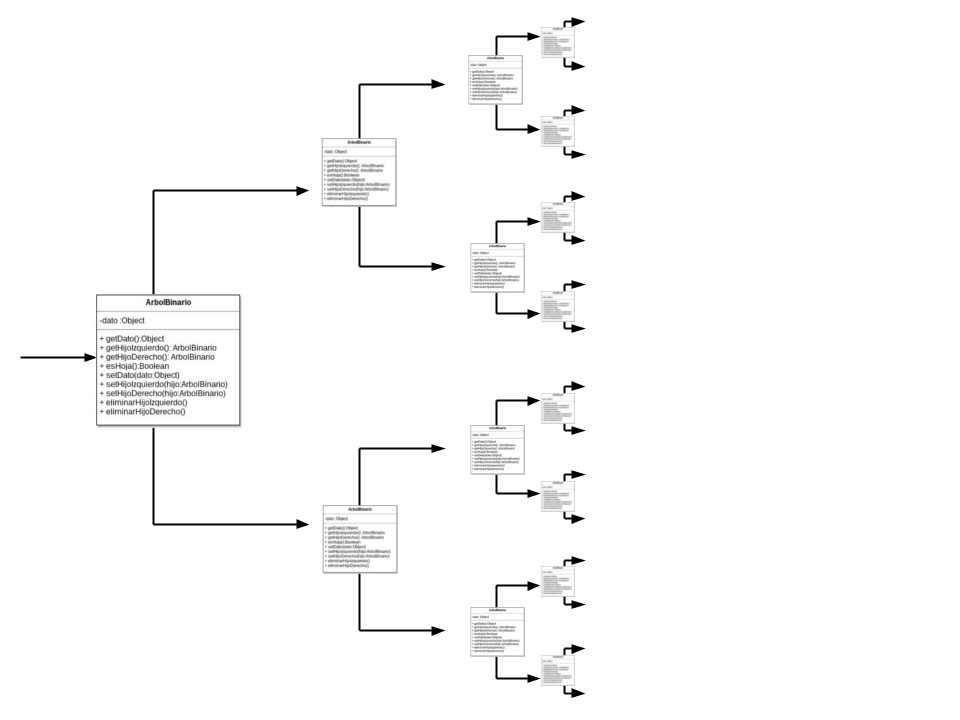
Heap

Definición

Propiedad estructural:

Es un árbol binario completo

Propiedad de orden:

MinHeap
* El elemento mínimo está almacenado en la raíz
* El dato almacenado en cada nodo es menor o igual al de sus hijos

MaxHeap
Al reves

Dado que un árbol binario completo es una estructura de datos regular, puede almacenarse en un arreglo, tal que:

La raíz está almacenada en la posición 1
Para un elemento que está en la posición i:
* El hijo izquierdo está en la posición 2*i
* El hijo derecho está en la posición 2*i + 1
* El padre está en la posición i/2

Insert

* se inserta al final
* hay que acomodar el arbol para que se conserve la propiedad de orden (percolate up)

Delete min/max

* se elimina la raíz (es siempre el min/max)
* se mueve el último elemento
* hay que acomodar el arbol para que se conserve la propiedad de orden (percolate down)

Tiempo de Ejecución

Repaso

Cuando intentamos encontrar la complejidad de un algoritmo, no nos interesa el número exacto de las operaciones realizadas, Sino la relación entre el número de operaciones y el tamaño del problema a medida que el tamaño crece.

Y nos interesa sobre todod el peor caso, es decir el número máximo de operaciones posibles para un tamaño determinado.

caso 1: operación Stack.pop()

¿cómo es la relación entre cantidad de operaciones y el tamaño de la pila?


Constante o de Orden(1)

siempre tarda lo mismo, independientemente de cuantos elementos haya en la pila

caso 2: búsqueda en una lista simple

¿Cómo es la relación entre cantidad de operaciones y el tamaño de la lista?


Lineal o de Orden(N)

cuando la cantidad de elementos de la lista crece, la cantidad de operaciones básicas crece de manera proporcional a N (si con un elemento se requiren 5 operaciones, con 2 van a ser 10, con 3 => 15, con 4 => 20, ... , N => 5N)

caso 3: búsqueda binaria en una lista

¿cómo es la relación entre cantidad de operaciones y el tamaño del árbol?


Logarítmica o de Orden log(N)

cuando la cantidad de elementos de la lista crece, la cantidad de operaciones básicas crece en proporción al logaritmo de N. (si para 1 elemento se requiren 2 op, 16 elementos => 2*4 op, 32 => 2*5, 64 => 2*6, ... N => 2*log(N) )

Funciones características

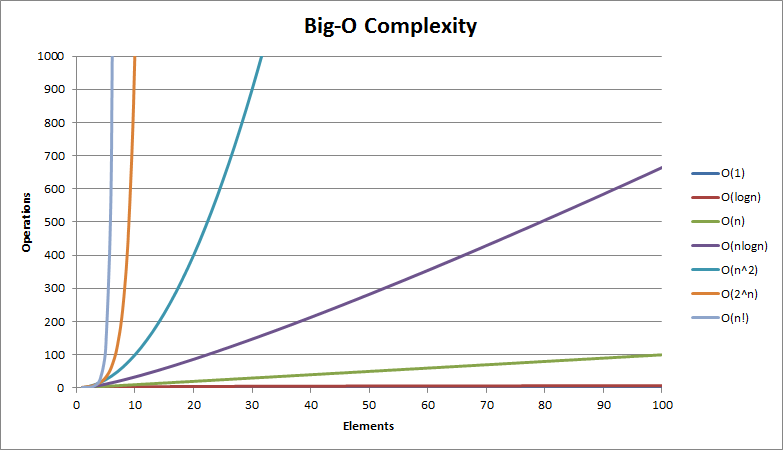
Big-O

Notación formal para expresar con precisión esa relación

Primero...

¿qué es T(n)

una función

¿y una función?

una asociación un valor de entrada con uno de salida

ahora...

n, log(n), n², ¿Son valores?


NO, son funciones.
Por lo tanto, T(n) es una funcion que devuelve una funcion! (higher order function, o función de orden superior)

Big O

definición:

Una función T(N) es O(f(N)) si existen las constantes C y n0 tal que:

T(N) <= C * f(N)


para todo N >= n0


Se lee: T de N es de Orden F de N

¿Quéééé?

¿Qué significa?

  1. Que la complejidad exacta de un algoritmo, es función del tamaño del problema ( T(N) )
  2. Y que f(N) es una cota superior de dicha complejidad. Es decir, que en el peor caso , la complejidad del algoritmo nunca va a ser mayor que f(N).


La forma más fácil de entenderlo es ponerle números a las constantes y a F(n)

T(N) de algoritmos iterativos

T(N) de algoritmos recursivos 


            def potencia(x, n):
              if(n == 0):
                return 1
              else:
                return x * potencia(x, n-1)

Pasos

1. identificar la variable libre (N)
2. Identificar T(n) para el caso base
3. Encontrar la expresión genéral de la recursión
4. Reemplazar T(N) del caso base en la expresión general\
5. partienddo de la definición de T(N), expresar el tiempo de ejecución usando big-o
  1. t(0) = O(1)
  2. t(n) = t(n-1) + 2

            t(n-1) = t(n-2) + 2
            
          reemplazamos t(n-1) en 1.
            
          t(n) = [  t(n-1)  ] + 2
          t(n) = [t(n-2) + 2] + 2
            
                t(n-2) = t(n-3) + 2
      
                t(n) = [  t(n-2)  ] + 2 + 2
                t(n) = [  t(n-2)  ] + 2 + 2
      
                t(n) = [t(n-3) + 2] + 2 + 2
                t(n) = t(n-3) + 2*3
                
                t(n-3) = [t(n-4) + 2]
      
              t(n) = t(n-4) + 2 + 3*2
              t(n) = t(n-4) + 4*2

en general 

              t(n) = t(n-i) + 2 * i
  1. t(0) = O(1)
  2. t(n) = t(n-i) + 2*i


ya sabemos que T(0) es 1
¿Qué valor debería tener n, para que t(n-i) sea t(0)?
Igualamos (n - i) = 0 y despejamos i 
              n - i = 0
            
              # si despejamos i
              
              i = n
              
              # reemplazamos i en la expresión general de la recurrencia:
              t(n) = t(n-i) + 2 * i
              t(n) = t(n - n) + 2 * n
              t(n) = t(0) + 2*n
              t(n) = 1 + 2*n
              
              T(n) = O(n)
En la página tienen disponible un Apunte con las explicaciones prácticas acerca del cálculo de T(n) iterativo y recurrente.

Algunas referencias

http://web.mit.edu/16.070/www/lecture/big_o.pdf http://courses.csail.mit.edu/6.01/spring07/lectures/lecture4.pdf http://www.lab.dit.upm.es/~lprg/material/apuntes/o/#s2 http://en.wikipedia.org/wiki/Big_O_notation http://www.cs.ucf.edu/~dmarino/ucf/cop3502/lec_biswas/recursion12.pdf

Fin

¿Preguntas?