Estructuras de Datos y Algoritmos II

Clase 1

versión imprimible o pfd

¿Por qué?

Problema

El placard

¿qué pasa si tenemos sólo un estante, largo, pero que no entra mas de una prenda de alto ?

¿y si la puerta es muy pequeña, y adentro hay un perchero giratorio?

condicionantes, requerimientos

¿Qué es una estructura de datos?

“ Una estructura de datos es una forma particular de organizar la información en una computadora de manera tal que pueda se usada eficientemente. ” Paul E. Black - "Dictionary of Algorithms and Data Structures"

“ Una estructura de datos es una forma de almacenar y organizar información para facilitar el acceso y las modificaciones. ”
[Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein] - "Introduction to algorithms"

Propiedades Reglas Restricciones

¿Qué es un algoritmo?

“ un algoritmo es un procedimiento (computacional) bien definido que toma un valor/es como entrada y produce un valor/es como salida. Es por lo tanto una secuencia de pasos que transforman una entrada en una salida. ”

“ También puede verse como una herramienta para resolver un problema computacional bien especificado. ”

¿Por qué?

“ frecuentemente tendremos que identificar y balancear las ventajas y desventajas acerca de una solución. Como científicos de la computación, además de nuestra habiliadad de resolver problemas, también necesitaremos conocer herramientas y técnicas para evaluar dichas soluciones. A la larga, generalemente existen muchas formas de resolver un problema determinado. Encontrar una solución y decidir si es una buena solución, son tareas que realizaremos una y otra vez. ” "Introduction to algorithms", Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein

“ (...) No existe una estructura de datos que funcione bien para todos los propósitos, por lo tanto es importante conocer las fortalezas y limitaciones de varias de ellas. ” ibidem

¿Cómo determinamos qué estructura de datos y qué algoritmos son mejores para solucionar un problema determinado?

No vamos a estudiar todas estructuras de datos y todos los tipos de algoritmos. El propósito de la materia es construir herramientas conceptuales y prácticas que aporten a responder estas preguntas.

Estructuras de Datos y Algoritmos II

Profesores:

Emanuel Borda

Fernando Martínez

Página:

edya2upe.github.io

Temas y fechas

#Clase	Fecha	   Tema                  TP
1	22/3/2016  Pilas, colas, listas  #1
2	29/3/2016  Objetos y T(n)	 #1
3	05/4/2016  AB AVL T(n)	         Examen TP 1 - Comienzo TP2
4	12/4/2016  AB AVL T(n)	         #2
5	19/4/2016  AB AVL T(n)	         #2
6	26/4/2016  Heap AG T(n)	         Examen TP2 - Comienzo TP3
7	03/5/2016  Heap AG T(n)	         #3
8	10/5/2016  Heap AG T(n)	         #3
9	17/5/2016  Grafos	         Examen TP3 - Comienzo TP4
10	24/5/2016  Grafos	         #4
11	31/5/2016  Grafos	         #4
12	07/6/2016  Consulta 	         Examen TP4
13	14/6/2016  Consulta General
14	21/6/2016  Recuperatorio General

Modalidad de cursada

1 evaluación por práctica
1 recuperatorio general
Promoción: todos las evaluaciones aprobadas

Listas

¿Qué es una lista?

Definición

Una lista es una coleccion de elementos donde cada uno mantiene una posicion relativa respecto a los otros. Es decir, entre los elementos que la componen existe una relación de orden (primero, segundo, tercero... último).

Estructura lineal, tiene un principio y un final.

Es una estructura de datos simple que puede servir para construir otras estructuras de datos más complejas

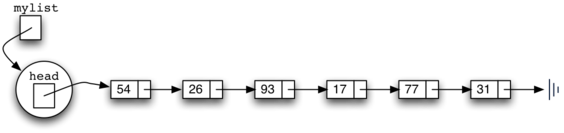
¿Qué cosas podemos hacer con una lista?

¿de que manera podemos acceder a qué datos?

¿Cómo la modificamos?

Operaciones sobre listas

size
empty
first()
last()
get(index)
find(item)
index(item)
includes(item)

insert(item, position)
append(item)
prepend(item)
remove(item)
clear()

Tipos de listas

Dependiendo cómo se organicen los elementos podemos plantear distintos tipos de listas:

lista enlazada simple (linked list)
lista enlazada doble (double linked list)
lista circular (circular list)
lista no ordenada (unordered)
lista ordenada (sorted)

https://en.wikipedia.org/wiki/Linked_list

Otras estructuras lineales

pilas (stack)
colas (queue)
colas dobles (dequeue)
arreglos (array) (estáticos y dinámicos)

Pilas

operaciones:

push(item)
pop()
top()

Colas

operaciones:

push(item)
pop()
top() (o first())
last()

podemos decir que tanto pilas como colas son un subconjunto de las listas

Arreglos (Array)

Estructura de datos de bajo nivel
Almacena un conjunto de objetos en posiciones contiguas de memoria.
Indexada. Es decir puede accederse a cada uno de los elementos mediante un índice (suelen ser numéricos)
Pueden ser estáticos o dinámicos.

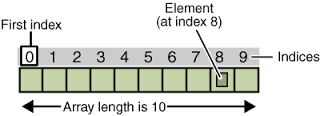
operaciones básicas:

acceder a un valor (suele escribirse a[1])
setear un valor (suele escribirse como una asignacion a[1] = item)
size o length

Arreglos (Array)

Entre las propiedades mas importantes encontramos: acceso directo
(simplemente es necesario acceder a la posicion de memoria que contiene el valor que quiero leer)

Clase 1

Parte 2

Repaso

Recursión

Recurrencia, recursión o recursividad es la forma en la cual se especifica un proceso basado en su propia definición.

Expresar un problema en instancias más pequeñas de sí mismo, hasta llegar a una que tenga solución trivial

Recursión

Caso base
Llamado recursivo

Sumar todos los elementos de una lista


def sum(list)
    if(len(list) == 0):
        return 0
    else:
        value = list.pop()
        return value + sum(list)

print sum([1,1,1,1,1,1])

Contar todos los elementos de una lista


def count(list, total=0):
    if(len(list) == 0):
        return total
    else:
        total = total + 1
        a.pop()
        count(a, total)
        return total

print count([1,2,3,4,5,6])

Programación Orientada a Objetos

Objetos
Métodos
Clases
Herencia

Programación Orientada a Objetos

Abstracción
Encapsulamiento
Polimorfismo

Objetos, Métodos, Atributos


frodo = Hobbit("frodo")
gollum = Hobbit("gollum")
my_precious = Ring()
sting = Sword()

frodo.wear(my_precious)
frodo.weapon = sting
gollum.attack(frodo)
frodo.attack(gollum)

Clases


class Hobbit(name):
  self.name = name
  self.equipement = []
  self.weapon = None

  def wear(self, an_item):
    equipment.push(an_item)

  def attack(self, creature):
    if self.weapon == None
       self.punch(creature)
    else:
       self.weapon.attack(creature)

Tiempo de Ejecución

Eficiencia

"la eficiencia algorítmica describe aquellas propiedades de los algoritmos que están relacionadas con la cantidad de recursos utilizados por el algoritmo. Un algoritmo debe ser analizado para determinar el uso de los recursos que realiza"

recursos

CPU, Memoria, Disco, Red, Etc...

vamos a medir la complejidad algorítmica (uso del cpu)

Enfoque teórico

El tiempo requerido por una función es proporcional a la cantidad de operaciones básicas que realiza.

una operación artimética ( +, *, -, /).
una asignación
un test (if(x = 0) )
una lectura
una escritura

No nos interesa el número EXACTO de las operaciones realizadas, sino la RELACIÓN entre el número de operaciones y el tamaño del problema.

Nos interesa sobre todo el PEOR CASO , es decir el número MÁXIMO de operaciones posibles para un tamaño determinado.

Funciones características

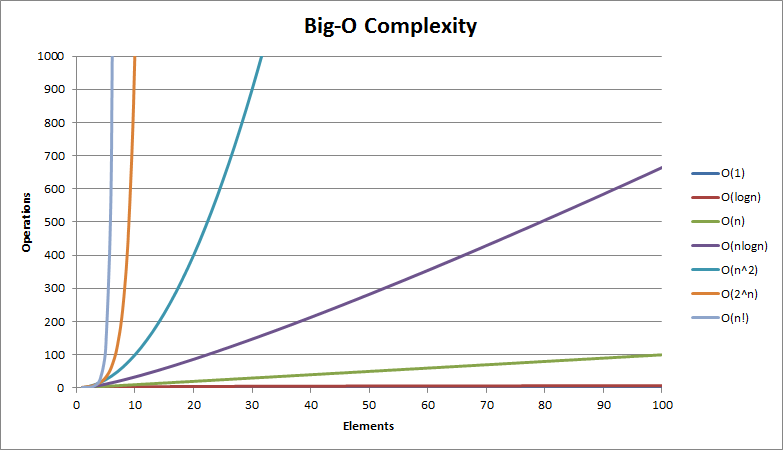
Cómo calculamos T(N)

secuencia de sentencias

 
            sentencia 1
            sentencia 2
            sentencia 3

T(N) = T(sentencia 1) + T(sentencia 2) + T(sentencia 3)

si las sentencias están todas construidas por sentencias básicas,
entonces es el tiempo de cada sentencias es O(1)
por lo tanto, la suma total también es O(1)

condicional


            if(cond):
               bloque 1;
            else:
               bloque 2;

T(N) = max(t(bloque 1), t(bloque 2))

Dado que o bien ejecuta el bloque 1 o bien el bloque 2
y que tenemos en cuenta el peor caso.

Loops (for, while, etc)

 
            for i in range(1..n):
                secuencia;

T(N) = N * T(secuencia)

El bucle se ejecuta N veces, por lo tanto la secuencia se ejecuta N veces
si T(secuencia) O(1) => el bucle es N * O(1) => O(N)

Bucles anidados

 
            for i in range(1..n):
               for j in range(1..m):
                  secuencia;

El for externo se ejecuta n veces,
para cada iteración del for externo hay m iteraciones del interno
las sentencias se ejecutan n * m veces
si las consideramos O(1)

Tiempo total: O(n * m)
si m = n, entoces total O(n²)

Fin

¿Preguntas?